Case study: hypothesis testing and strategy optimization
11 Aug 2021This case study is one of the take-home assignment provided by Starbucks for their job candidates. It is a great example of 1) hypothesis testing and 2) machine learning in business analytics. More specifically, hypothesis testing was performed to evaluate data gathered from A/B testing, and determine levels of significance for the business metrics of interest. Following the evaluations, the conclusions were further used to inform and optimize Ad campaign strategy to improve the business metrics.
Background information
The data for this exercise consists of about 120,000 data points split in a 2:1 ratio among training and test files. In the experiment simulated by the data, an advertising promotion was tested to see if it would bring more customers to purchase a specific product priced at $10. Since it costs the company 0.15 to send out each promotion, it would be best to limit that promotion only to those that are most receptive to the promotion. Each data point includes one column indicating whether or not an individual was sent a promotion for the product, and one column indicating whether or not that individual eventually purchased that product. Each individual also has seven additional features associated with them, which are provided abstractly as V1-V7.
Evaluation metrics
The task is to use the training data to understand what patterns in V1-V7 to indicate that a promotion should be provided to a user. Specifically, the goal is to maximize the following metrics:
- Incremental Response Rate (IRR)
IRR depicts how many more customers purchased the product with the promotion, as compared to if they didn’t receive the promotion. Mathematically, it’s the ratio of the number of purchasers in the promotion group to the total number of customers in the purchasers group (treatment) minus the ratio of the number of purchasers in the non-promotional group to the total number of customers in the non-promotional group (control).
\[IRR = \frac{purch_{treat}}{cust_{treat}} - \frac{purch_{ctrl}}{cust_{ctrl}}\]- Net Incremental Revenue (NIR)
NIR depicts how much is made (or lost) by sending out the promotion. Mathematically, this is 10 times the total number of purchasers that received the promotion minus 0.15 times the number of promotions sent out, minus 10 times the number of purchasers who were not given the promotion.
\[NIR = (10\cdot purch_{treat} - 0.15 \cdot cust_{treat}) - 10 \cdot purch_{ctrl}\]Case study workflow
- Inspect the data and perform EDA to check for data type, any null values, as well as determine the features and labels for each observations.
- Analyze the current A/B testing result, and retrieve IRR and NIR values. This step will include validating group assignment by checking invariant metric (proportion of control group), and checking the significance levels of the obtained evaluation metrics.
- Draw conclusion of current A/B testing results.
- Optimize promotion strategy using ML models, and evaluate obtained classifiers.
1. Inspect the Data
The training data set contains 84543 observations with 7 features and contains no null values. Each observation corresponds to an individual customer and the features associated with each sample are attributes for that customer. Feature V2 and V3 are continuous quantitative variables. However, V1, V4 through V7 are discrete quantitative variables, indicating those might be categorical variables and need proper encoding in step 4.
train_data = pd.read_csv('./training.csv')
train_data.head()
| ID | Promotion | purchase | V1 | V2 | V3 | V4 | V5 | V6 | V7 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | No | 0 | 2 | 30.443518 | -1.165083 | 1 | 1 | 3 | 2 |
| 1 | 3 | No | 0 | 3 | 32.159350 | -0.645617 | 2 | 3 | 2 | 2 |
| 2 | 4 | No | 0 | 2 | 30.431659 | 0.133583 | 1 | 1 | 4 | 2 |
| 3 | 5 | No | 0 | 0 | 26.588914 | -0.212728 | 2 | 1 | 4 | 2 |
| 4 | 8 | Yes | 0 | 3 | 28.044332 | -0.385883 | 1 | 1 | 2 | 2 |
train_data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 84534 entries, 0 to 84533
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 ID 84534 non-null int64
1 Promotion 84534 non-null object
2 purchase 84534 non-null int64
3 V1 84534 non-null int64
4 V2 84534 non-null float64
5 V3 84534 non-null float64
6 V4 84534 non-null int64
7 V5 84534 non-null int64
8 V6 84534 non-null int64
9 V7 84534 non-null int64
dtypes: float64(2), int64(7), object(1)
memory usage: 6.4+ MB
2. Analyze experiment results
2.1 Calculate IRR and NIR based on experiment results
This step is fairly straight forward by following the definitions of IRR and NIR. It was determined that:
Incremental Response Rate (IRR) from the experiment: 0.00945
Net Incremental Revenue (NIR) from the experiment: -2334.60
2.2 Check invariant metric
In this experiment, the metrics to determine the effect of promotions to customers on the purchasing behavior of this $10 item. Before jumping into analyzing the effect, we first need to check if the assignments of promotion to customers was random, i.e. checking the invariant metric. We can use \(\alpha\) = 0.05 as the significance level.
\[\begin{align} H_0: p_{ctrl} - 0.5 = 0 \\ H_a: p_{ctrl} - 0.5 \neq 0 \end{align}\]There are two approaches we could perform this hypothesis testing via analytical method and simulation.
Since the assignment of control and treatment group follows binomial distributions, analytical method can be used. Following the analytical approach, p-val of 0.5068 is obtained.
On the other hand, simulation or non-parametric methods such as bootstrapping can be used to estimate test statistics. This type of methods does not rely on assumptions on distributions. Based off Law of Large Numbers and its closest cousin Central Limit Theorem, modern computing power enables us to use bootstrapping to obtain a good estimate on test statistics, such as means, differences in means, as well as proportion and difference in proportions.
In this case study, we could first obtain observed difference between the sample and null hypothesis as:
p_ctrl = num_ctrl / num_obs
obs_diff = p_ctrl - 0.5
obs_diff
-0.0011474672912674122
After performing bootstrapping for 10000 times, we could get the distributions for sample proportion differences for null hypothesis as well as observed samples.
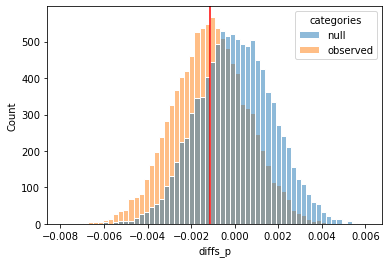
Figure 1. distributions for sample proportion differences for null hypothesis and observed samples.
Based on this result, we could estimate the p-val as follows:
p_val = (null_p>-obs_diff).mean() + (null_p < obs_diff).mean()
print("p-value for the invariant metric: {:.4f}".format(p_val))
p-value for the invariant metric: 0.5121
Conclusion: Based on results from analytical method and simulation, using a \(\alpha\) = 0.05, we failed to reject the null hypothesis. In this experiment, there was not a significant difference in the number of customers assigned to the control and treatment group, and it is safe to proceed to check evaluation metrics, such as IRR and NIR, using this experiment result to see whether the differences are significant.
2.3 Check evaluation metric
Since we are using IRR and NIR to determine if the promotion has a significant effect on purchase, we are performing mutiple comparsions. Therefore the significance level for each test needs to be corrected. Using Bonferroni correction and a total signifcance level of 0.05, we can use \(\alpha\) = 0.025 for each test.
2.3.1 IRR
\[\begin{align} IRR = p_{pur\_treat} - p_{pur\_ctrl} \\ H_0: IRR \leq 0\\ H_a: IRR > 0 \end{align}\]Again, using the analytical approach, p-val for the IRR is shown to be 0. Bootstrapping was also used to estimate the p-val. The distribution of IRR under observed sample and null hypothesis is shown below:
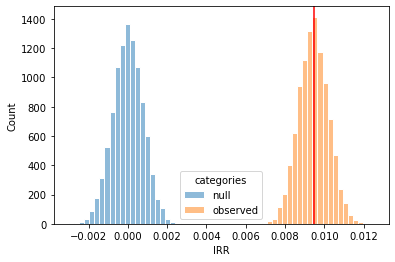
Figure 2. distributions for IRR for null hypothesis and observed samples.
Based on this result, we could estimated the p-val as follows:
p_val = (null_irr > obs_irr).mean()
print("p-value for the IRR: {:.4f}".format(p_val))
p-value for the IRR: 0.0000
Conclusion: based on the this result, using a \(\alpha\) = 0.025, we reject the null hypothesis.
In this experiment, there was a significant increase in IRR. Relate back to the definition of IRR, it depicts how many more customers purchased the product with the promotion, as compared to if they didn’t receive the promotion. This result indicated that promotion is a great strategy in increasing number of purchase of this product, and the increase is significant.
2.3.3 NIR
\(\begin{align} \begin{gathered} NIR = (num_{treat\_purch} \times 10 - num_{treat} \times 0.15)-num_{treat\_purch} \times 10\\ H_0: NIR \leq 0\\ H_a: NIR > 0 \end{gathered} \end{align}\) Simulation using bootstrapping was used to estimate the p-val for NIR. The distribution of NIR under observed sample and null hypothesis is shown below:
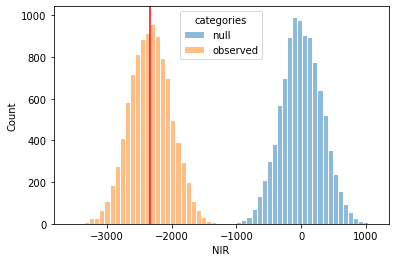
Figure 3. distributions for NIR for null hypothesis and observed samples.
Based on this result, we could estiamted the p-val as follows:
p_val = (null_nir>obs_nir).mean()
print("p-value for the NIR: {:.4f}".format(p_val))
p-value for the NIR: 1.0000
Conclusion: based on the this result, using a \(\alpha\) = 0.025, we failed to reject the null hypothesis.
In this experiment, there was a not significant increase in NIR. Relate back to the definition of NIR, it depicts how much is made (or lost) by sending out the promotion. This result indicated that promotion does not increase NIR significantly.
3. Implication of current A/B test result
By looking at above test results, if we were to design the testing conditions differently, we could see that current assignment of promotion to customers actually created significant loss. Therefore, it is necessary to revisit the promotion strategy, which will be the focus of next section.
4. Optimize promotion strategy
The overall process of finding the optimized promotion strategy is by utilizing machine learning models.
- Train the classifier using the customer who actually made the purchase. Identify pattern of those who are willing to purchase this item.
- The idea behind this is, when a new customer feature set comes in, the classifier will classify if this customer is willing to purchase this item. If yes, then a promotion will be send out.
For those reasons, “purchase” column will be used as the label. After further examining the data set, it was found out that this data set is imbalanced, which needs balancing by making the # of observations similar for purchasing and non-purchasing customers.
In addition, categorical features were encoded with dummy variables using pandas get_dummies() as follows:
sample_train_data= pd.get_dummies(sample_train_data, columns=['V1', 'V4', 'V5', 'V6', 'V7'], drop_first=True)
A train_test_split was performed using scikit-learn’s model_selection module. The training data was fed into a LogisticRegression classifier. The trained model was used in generating promotion strategies.
Testing suit was provided to evaluate generated strategy, comparing the our model with a benchmark.
Using the strategy generated by trained model, we have:
\[\begin{align} \begin{gathered} IRR = 0.0189 \\ NIR = 354.20 \end{gathered} \end{align}\]Compared with benchmark, where IRR = 0.0188 and NIR = 189.45. With similar IRR, our strategy achieved 87% increase in NIR. Therefore, our promotion strategy targets more to the customers who are willing to purchase this new $10 item.
Case study conclusion
This case study demonstrated the workflow of experimental design, hypothesis testing, and machine learning in optimizing business strategy. Use of inferential statistics to gain insights of the population and machine learning to understand individual preferences is critical in creating an effective business strategy.
Acknowledgments
Dataset is provided by Udacity Data Scientist Nanodegree program